Достаточно часто при анализе экономических систем приходится решать так называемые задачи массового обслуживания, возникающие в следующей ситуации. Пусть анализируется система технического обслуживания автомобилей, состоящая из некоторого количества станций различной мощности. На каждой из станций (элемента системы) могут возникать, по крайней мере, две типичные ситуации:
- число заявок слишком велико для данной станции, возникают очереди, и за задержки в обслуживании приходится платить;
- на станцию поступает слишком мало заявок и теперь уже приходится учитывать потери, вызванные простоем станции.
Ясно, что цель системного анализа в данном случае заключается в определении некоторого соотношения между потерями доходов по причине очередей и потерями по причине простоя станций.
Теория массового обслуживания – специальный раздел теории систем – это раздел теории вероятности, в котором изучаются системы массового обслуживания с помощью математических моделей.
Система массового обслуживания (СМО) – это модель, включающая в себя: 1) случайный поток требований, вызовов или клиентов, нуждающихся в обслуживании; 2) алгоритм осуществления этого обслуживания; 3) каналы (приборы) для обслуживания.
Примерами СМО являются кассы, АЗС, аэропорты, продавцы, парикмахеры, врачи, телефонные станции и другие объекты, в которых осуществляется обслуживание тех или иных заявок.
Задача теории массового обслуживания состоит в выработке рекомендаций по рациональному построению СМО и рациональной организации их работы с целью обеспечения высокой эффективности обслуживания при оптимальных затратах.
Главная особенность задач данного класса – явная зависимость результатов анализ и получаемых рекомендаций от двух внешних факторов: частоты поступления и сложности заказов (а значит и времени их исполнения).
Предмет теории массового обслуживания – это установление зависимости между характером потока заявок, производительностью отдельного канала обслуживания, числом каналов и эффективностью обслуживания.
В качестве характеристик СМО рассматриваются:
- средний процент заявок, получающих отказ и покидающих систему не обслуженными;
- среднее время «простоя» отдельных каналов и системы в целом;
- среднее время ожидания в очереди;
- вероятность того, что поступившая заявка будет немедленно обслужена;
- закон распределения длины очереди и другие.
Добавим, что заявки (требования) поступают в СМО случайным образом (в случайные моменты времени), с точками сгущения и разрежения. Время обслуживания каждого требования также является случайным, после чего канал обслуживания освобождается и готов к выполнению следующего требования. Каждая СМО, в зависимости от числа каналов и их производительности, обладает некоторой пропускной способностью. Пропускная способность СМО может быть абсолютной (среднее число заявок, обслуживаемых в единицу времени) и относительной (среднее отношение числа обслуженных заявок к числу поданных).
3.1 Модели систем массового обслуживания.
Каждую СМО может характеризовать выражением: ( a / b / c ) : ( d / e / f ), где
a - распределение входного потока заявок;
b - распределение выходного потока заявок;
c – конфигурация обслуживающего механизма;
d – дисциплина очереди;
e – блок ожидания;
f – емкость источника.
Теперь рассмотрим подробнее каждую характеристику.
Входной поток заявок – количество поступивших в систему заявок. Характеризуется интенсивностью входного потока l.
Выходной поток заявок – количество обслуженных системой заявок. Характеризуется интенсивностью выходного потока m.
Конфигурация системы подразумевает общее число каналов и узлов обслуживания. СМО может содержать:
- один канал обслуживания (одна взлетно-посадочная полоса, один продавец);
- один канал обслуживания, включающий несколько последовательных узлов (столовая, поликлиника, конвейер);
- несколько однотипных каналов обслуживания, соединенных параллельно (АЗС, справочная служба, вокзал).
Таким образом, можно выделить одно- и многоканальные СМО.
С другой стороны, если все каналы обслуживания в СМО заняты, то подошедшая заявка может остаться в очереди, а может покинуть систему (например, сбербанк и телефонная станция). В этом случае мы говорим о системах с очередью (ожиданием) и о системах с отказами.
Очередь – это совокупность заявок, поступивших в систему для обслуживания и ожидающих обслуживания. Очередь характеризуется длиной очереди и ее дисциплиной.
Дисциплина очереди – это правило обслуживания заявок из очереди. К основным типам очереди можно отнести следующие:
- ПЕРППО (первым пришел – первым обслуживаешься) – наиболее распространенный тип;
- ПОСППО (последним пришел – первым обслуживаешься);
- СОЗ (случайный отбор заявок) – из банка данных.
- ПР – обслуживание с приоритетом.
Длина очереди может быть
- неограничена – тогда говорят о системе с чистым ожиданием;
- равна нулю – тогда говорят о системе с отказами;
- ограничена по длине (система смешанного типа).
Примером СМО с чистым ожиданием можно считать погрузочно-разгрузочное депо. В основном же ограничение на длину очереди накладывает размер места для размещения очереди (например, автостоянки или помещения).
Блок ожидания – «вместимость» системы – общее число заявок, находящихся в системе (в очереди и на обслуживании). Таким образом, е=с+d.
Емкость источника, генерирующего заявки на обслуживание – это максимальное число заявок, которые могут поступить в СМО. Например, в аэропорту емкость источника ограничена количеством всех существующих самолетов, а емкость источника телефонной станции равна количеству жителей Земли, т.е. ее можно считать неограниченной.
Количество моделей СМО соответствует числу всевозможных сочетаний этих компонент.
3.2 Входной поток требований.
С каждым отрезком времени [a,a+T ], свяжем случайную величину Х, равную числу требований, поступивших в систему за время Т.
Поток требований называется стационарным, если закон распределения не зависит от начальной точки промежутка а, а зависит только от длины данного промежутка Т. Например, поток заявок на телефонную станцию в течение суток (Т=24 часа) нельзя считать стационарным, а вот с 13 до 14 часов (Т=60 минут) – можно.
Поток называется без последействия, если предыстория потока не влияет на поступления требований в будущем, т.е. требования не зависят друг от друга.
Поток называется ординарным, если за очень короткий промежуток времени в систему может поступить не более одного требования. Например, поток в парикмахерскую – ординарный, а в ЗАГС – нет. Но, если в качестве случайной величины Х рассматривать пары заявок, поступающих в ЗАГС, то такой поток будет ординарным (т.е. иногда неординарный поток можно свести к ординарному).
Поток называется простейшим, если он стационарный, без последействия и ординарный.
Основная теорема. Если поток – простейший, то с.в. Х[a.a+T] распределена по закону Пуассона, т.е. ![]() .
.
Следствие 1. Простейший поток также называется пуассоновским.
Следствие 2. M(X)=M(Х[ a, a+T ] )=lT, т.е. за время Т в систему в среднем поступает lT заявок. Следовательно, за одну единицу времени в систему поступает в среднем l заявок. Эта величина и называется интенсивностью входного потока.
Рассмотрим ПРИМЕР.
В ателье поступает в среднем 3 заявки в день. Считая поток простейшим, найти вероятность того, что в течение двух ближайших дней число заявок будет не менее 5.
Решение.
По условию задачи, l=3, Т=2 дня, входной поток пуассоновский, n ³5. при решении удобно ввести противоположное событие, состоящее в том, что за время Т поступит меньше 5 заявок. Следовательно, по формуле Пуассона, получим 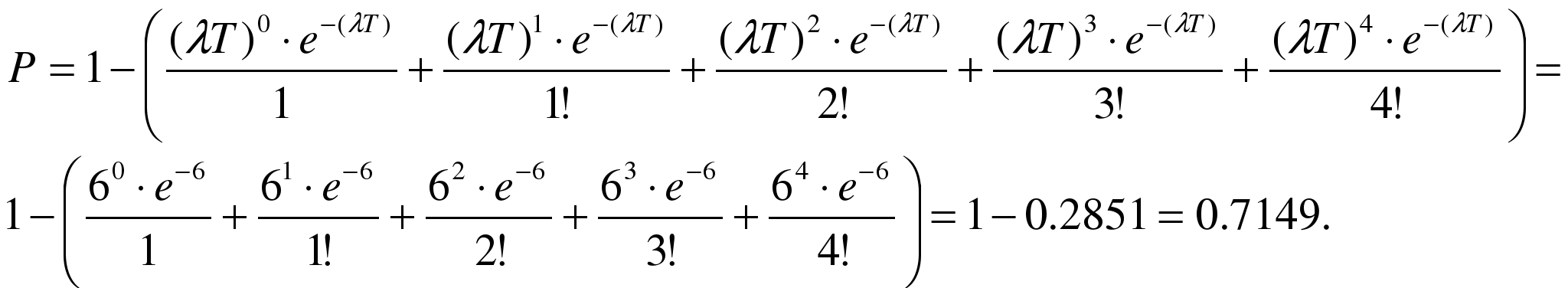
^
3.3 Состояние системы. Матрица и граф переходов.
В случайный момент времени СМО переходит из одного состояния в другое: меняется число занятых каналов, число заявок и очереди и пр. Таким образом, СМО с n каналами и длиной очереди, равной m, может находиться в одном из следующих состояний:
Е0 – все каналы свободны;
Е1 – занят один канал;
…
Еn – заняты все каналы;
Еn+1 – заняты все каналы и одна заявка в очереди;
…
Еn+m – заняты все каналы и все места в очереди.
Аналогичная система с отказами может находиться в состояниях E0 – En.
Для СМО с чистым ожиданием существует бесконечное множество состояний. Таким образом, состояниеEn СМО в момент времени t – это количество n заявок (требований), находящихся в системе в данный момент времени, т.е. n=n(t) – случайная величина, En(t) – исходы этой случайной величины, а Pn(t) – вероятность пребывания системы в состоянии En.
С состоянием системы мы уже знакомы. Отметим, что не все состояния системы равнозначны. Состояние системы называется источником, если система может выйти из этого состояния, но не может в него вернуться. Состояние системы называется изолированным, если система не может выйти из этого состояния или в него войти.
Для наглядности изображения состояний системы используют схемы (так называемые графы переходов), в которых стрелки указывают возможные переходы системы из одного состояния в другое, а также вероятности таких переходов.
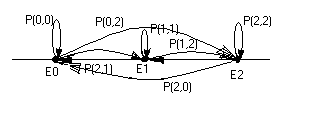
Рисунок 3.1 – граф переходов
| Сост. | Е0 | Е1 | Е2 | |
| Е0 | Р0,0 | Р0,1 | Р0,2 | |
| Е1 | Р1,0 | Р1,1 | Р1,2 | |
| Е2 | Р2,0 | Р2,2 | Р2,2 |
Также иногда удобно воспользоваться матрицей переходов. При этом первый столбец означает исходные состояния системы (текущие), а далее приведены вероятности перехода из этих состояний в другие.
Так как система обязательно перейдет из одного
состояния в другое, то сумма вероятностей в каждой строке всегда равна единице.
3.4 Одноканальные СМО.
3.4.1 Одноканальные СМО с отказами.
Будем рассматривать системы, удовлетворяющие требованиям:
(Р/Е/1):(–/1/¥). Предположим также, что время обслуживания требования не зависит от количества требований, поступивших в систему. Здесь и далее «Р» означает, что входной поток распределен по закону Пуассона, т.е. простейший, «Е» означает, что выходной поток распределен по экспоненциальному закону. Также здесь и далее основные формулы даются без доказательства.
Для такой системы возможно два состояния: Е0 – система свободна и Е1 – система занята. Составим матрицу переходов. Возьмем Dt – бесконечно малый промежуток времени. Пусть событие А состоит в том, что в систему за время Dt поступило одно требование. Событие В состоит в том, что за время Dt обслужено одно требование. Событие Аi,k – за время Dt система перейдет из состояния Ei в состояние Ek. Так как l – интенсивность входного потока, то за время Dt в систему в среднем поступает l*Dt требований. То есть, вероятность поступления одного требования Р(А)= l* Dt, а вероятность противоположного событияР(Ā)=1-l*Dt. Р(В)=F(Dt)=P(b<D t)=1-e-m D t=m Dt – вероятность обслуживания заявки за время Dt. Тогда А00 – заявка не поступит или поступит, но будет обслужена. А00=Ā+А*В. Р00=1-l*Dt. (мы учли, что(Dt)2 – бесконечно малая величина)
А01 – заявка поступит, но не будет обслужена. А01=А*![]() . Р01=l*Dt.
. Р01=l*Dt.
А10 – заявка будет обслужена и новой не будет. А10=В*Ā. Р10=m*Dt.
А11 – заявка не будет обслужена или поступит новая, которая еще не обслужена. А11=![]() +В*А. Р01=1-m*Dt.
+В*А. Р01=1-m*Dt.
Таким образом, получим матрицу переходов:
-
Сост. Е0 Е1 Е0 1-l*Dt l*Dt Е1 m*Dt 1-m*Dt
Вероятность простоя и отказа системы.
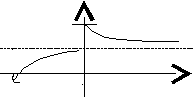
Найдем теперь вероятность нахождения системы в состоянии Е0 в любой момент времени t (т.е. р0 (t)). График функции ![]() изображен на рисунке 3.2.
изображен на рисунке 3.2.
Асимптотой графика является прямая ![]() .
.
Очевидно, начиная с некоторого момента t, ![]()
1
Рисунок 3.2
Окончательно получим, что ![]() и
и ![]() , где р1(t) – вероятность того, что в момент времени t система занята (т.е. находится в состоянии Е1).
, где р1(t) – вероятность того, что в момент времени t система занята (т.е. находится в состоянии Е1).
Очевидно, что в начале работы СМО протекающий процесс не будет стационарным: это будет «переходный», нестационарный режим. Спустя некоторое время (которое зависит от интенсивностей входного и выходного потока) этот процесс затухнет и система перейдет в стационарный, установившийся режим работы, и вероятностные характеристики уже не будут зависеть от времени.
Стационарный режим работы и коэффициент загрузки системы.
Если вероятность нахождения системы в состоянии Еk, т.е. Рk(t), не зависит от времени t, то говорят, что в СМО установился стационарный режим работы. При этом величина ![]() называется коэффициентом загрузки системы (или приведенной плотностью потока заявок). Тогда для вероятностейр0(t) и р1(t) получаем следующие формулы:
называется коэффициентом загрузки системы (или приведенной плотностью потока заявок). Тогда для вероятностейр0(t) и р1(t) получаем следующие формулы: ![]() ,
, ![]() . Можно также сделать вывод:чем больше коэффициент загрузки системы, тем больше вероятность отказа системы (т.е. вероятность того, что система занята).
. Можно также сделать вывод:чем больше коэффициент загрузки системы, тем больше вероятность отказа системы (т.е. вероятность того, что система занята).
ПРИМЕР.
На автомойке один блок для обслуживания. Автомобили прибывают по пуассоновскому распределению с интенсивностью 5 авто/час. Среднее время обслуживания одной машины – 10 минут. Найти вероятность того, что подъехавший автомобиль найдет систему занятой, если СМО работает в стационарном режиме.
Решение. По условию задачи, l=5, m =60мин/10мин = 6. Коэффициент загрузки y =5/6. Надо найти вероятность р1 – вероятность отказа системы. ![]() .
.
3.4.2 Одноканальные СМО с неограниченной длиной очереди.
Будем рассматривать системы, удовлетворяющие требованиям: (Р/Е/1):(d/¥/¥). Система может находиться в одном из состояний E0, …, Ek, … Анализ показывает, что через некоторое время такая система начинает работать в стационарном режиме, если интенсивность выходного потока превышает интенсивность входного потока (т.е. коэффициент загрузки системы меньше единицы). Учитывая это условие, получим систему уравнений
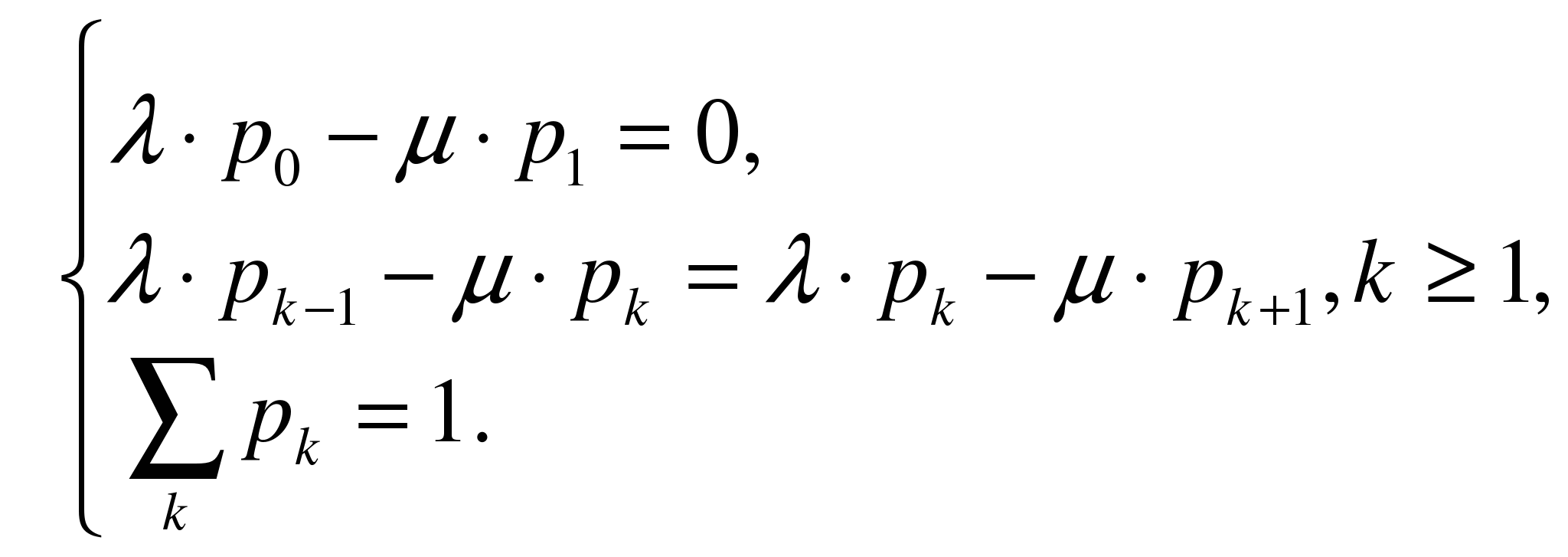
решая которую найдем, что ![]() . Таким образом, при условии, что y<1, получим
. Таким образом, при условии, что y<1, получим ![]() Окончательно,
Окончательно, ![]() и
и ![]() – вероятность нахождения СМО в состоянии Еk в случайный момент времени.
– вероятность нахождения СМО в состоянии Еk в случайный момент времени.
Средние характеристики системы.
За счет неравномерного поступления требований в систему и колебания времени обслуживания, в системе образуется очередь. Для такой системы можно исследовать:
- n – количество требований, находящихся в СМО (в очереди и на обслуживании);
- v – длину очереди;
- w – время ожидания начала обслуживания;
- w0 – общее время нахождения в системе.
Нас будут интересовать средние характеристики (т.е. берем математическое ожидание от рассматриваемых случайных величин, и помним, что y<1).
![]() – среднее число заявок в системе.
– среднее число заявок в системе.
![]() – средняя длина очереди.
– средняя длина очереди.
![]() – среднее время ожидания начала обслуживания, т.е. время ожидания в очереди.
– среднее время ожидания начала обслуживания, т.е. время ожидания в очереди.
![]() – среднее время, которое заявка проводит в системе – в очереди и на обслуживании.
– среднее время, которое заявка проводит в системе – в очереди и на обслуживании.
ПРИМЕР.
На автомойке один блок для обслуживания и есть место для очереди. Автомобили прибывают по пуассоновскому распределению с интенсивностью 5 авто/час. Среднее время обслуживания одной машины – 10 минут. Найти все средние характеристики СМО.
Решение. l=5, m =60мин/10мин = 6. Коэффициент загрузки y =5/6. Тогда среднее число автомобилей в системе ![]() , средняя длина очереди
, средняя длина очереди ![]() , среднее время ожидания начала обслуживания
, среднее время ожидания начала обслуживания ![]() часа = 50 мин, и, наконец, среднее время нахождения в системе
часа = 50 мин, и, наконец, среднее время нахождения в системе ![]() час.
час.
3.4.3 Одноканальные СМО смешанного типа.
Предположим, что длина очереди составляет m требований. Тогда, для любого s£ m, вероятность нахождения СМО в состоянии Е1+s, вычисляется по формуле 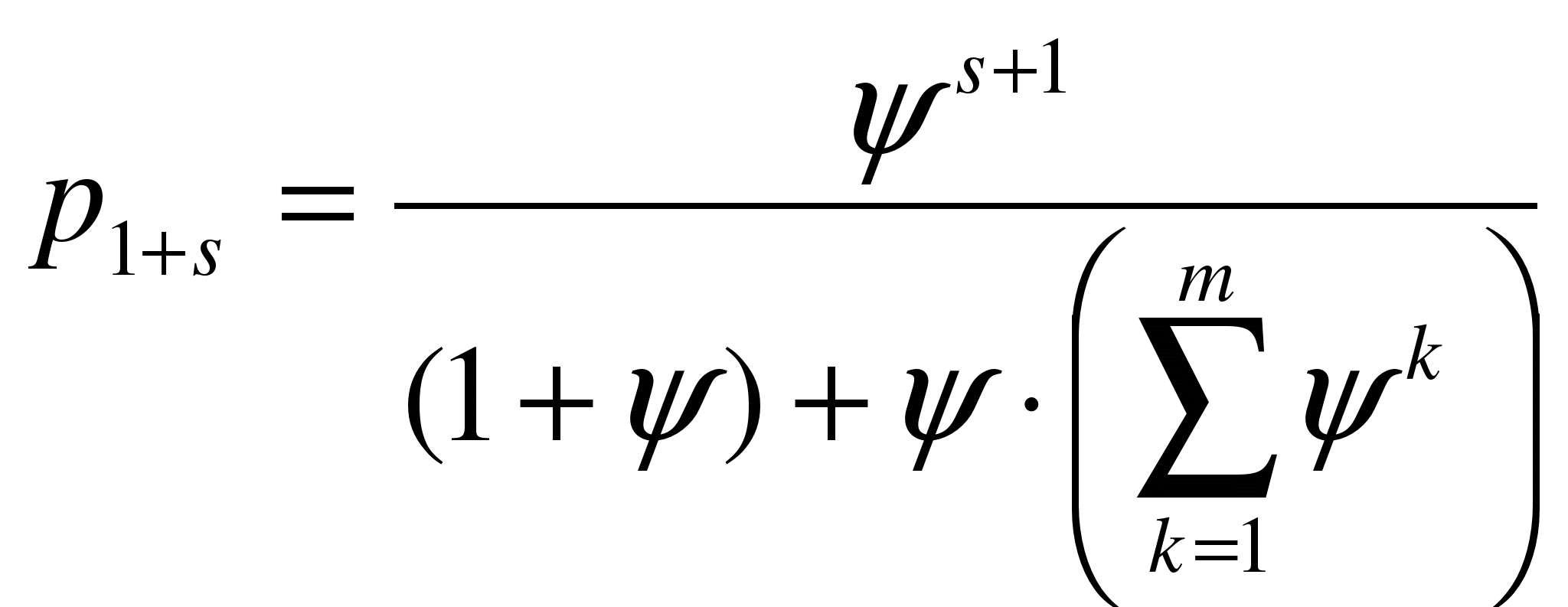 , т.е. одна заявка обслуживается и еще s заявок – в очереди.
, т.е. одна заявка обслуживается и еще s заявок – в очереди.
Вероятность простоя системы равна 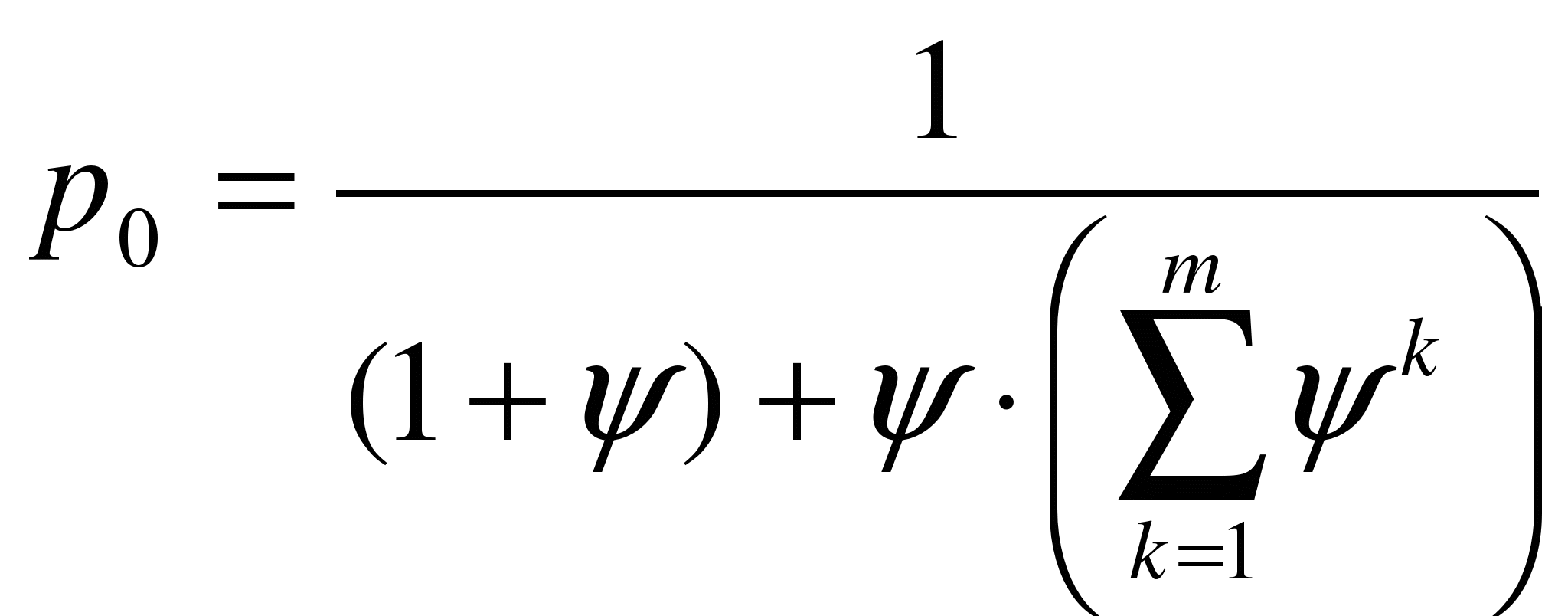 ,
,
а вероятность отказа системы - 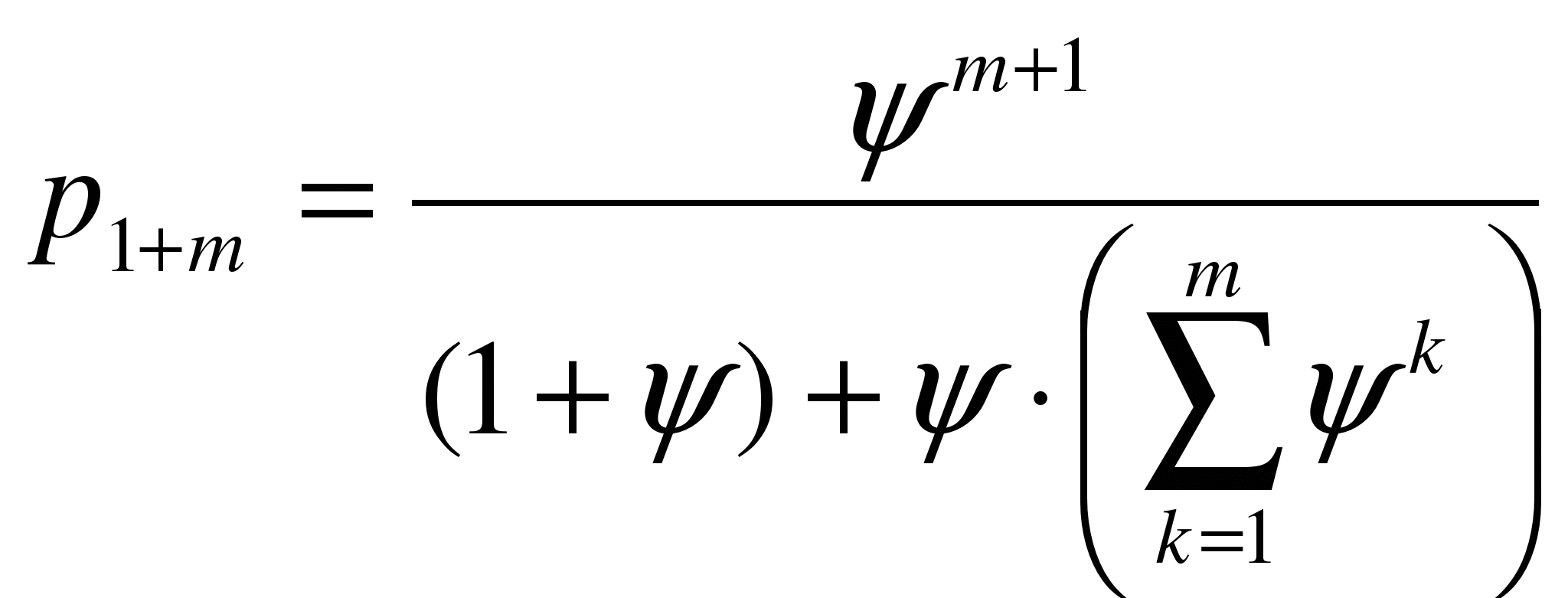 .
.
ПРИМЕР.
Даны три одноканальные системы, для каждой l=5, m =6. Но первая система – с отказами, вторая – с чистым ожиданием, а третья – с ограниченной длиной очереди, m=2. Найти и сравнить вероятности простоя этих трех систем.
Решение. Для всех систем коэффициент загрузки y =5/6. Для системы с отказами ![]() . Для системы с чистым ожиданием
. Для системы с чистым ожиданием ![]() . Для системы с ограниченной длиной очереди
. Для системы с ограниченной длиной очереди ![]() . Вывод очевиден: чем больше заявок находится в очереди, тем меньше вероятность простоя системы.
. Вывод очевиден: чем больше заявок находится в очереди, тем меньше вероятность простоя системы.
3.5 Многоканальные СМО.
3.5.1 Многоканальные СМО с отказами.
Будем рассматривать системы (Р/Е/s):(-/s/¥) в предположении, что время обслуживания не зависит от входного потока и все линии работают независимо. Многоканальные системы, помимо коэффициента загрузки, можно также характеризовать коэффициентом ![]() , где s – число каналов обслуживания. Исследуя многоканальные СМО, получим следующие формулы (формулы Эрлáнга) для вероятности нахождения системы в состоянии Еk в случайный момент времени:
, где s – число каналов обслуживания. Исследуя многоканальные СМО, получим следующие формулы (формулы Эрлáнга) для вероятности нахождения системы в состоянии Еk в случайный момент времени:
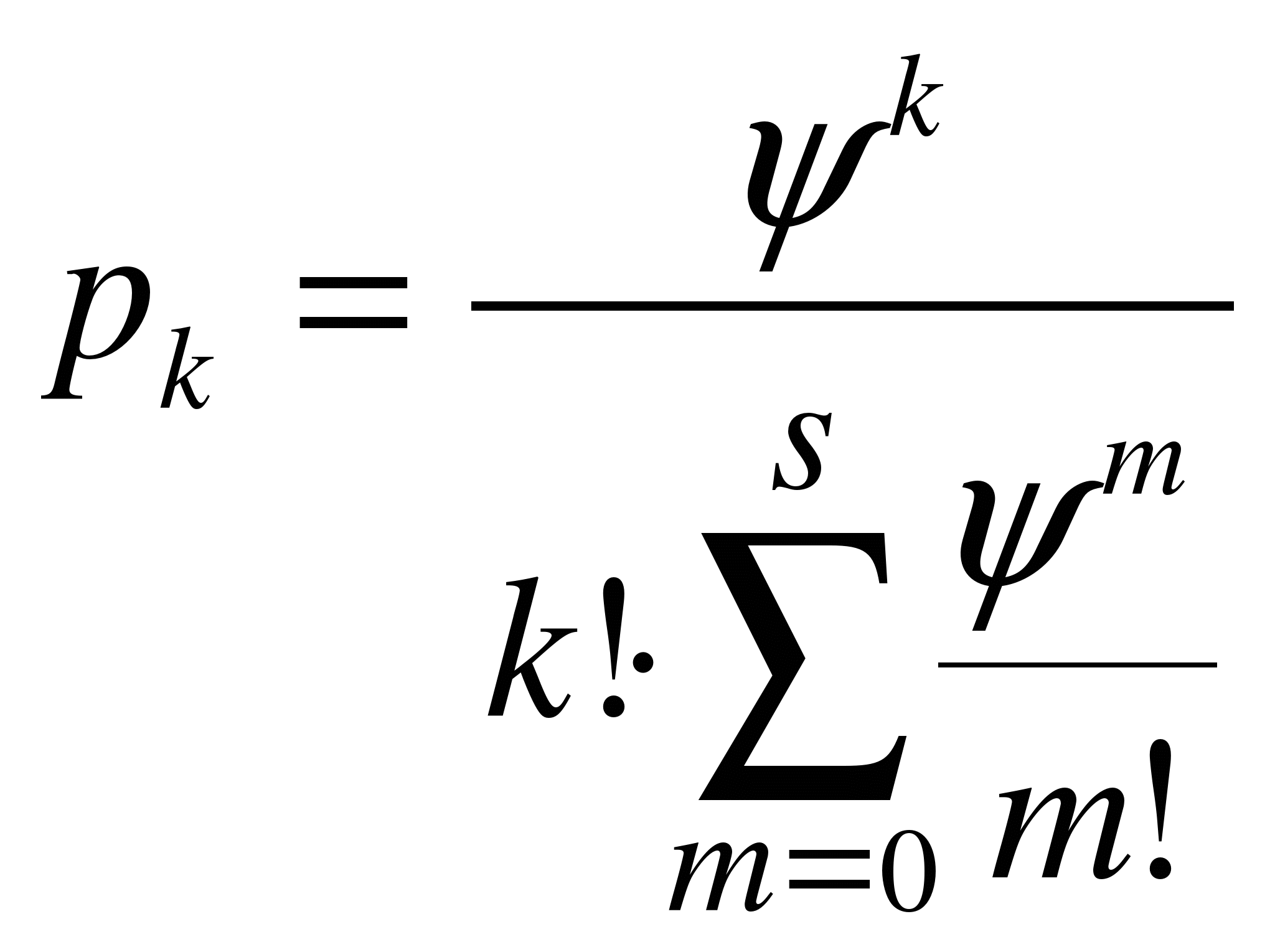 , k=0, 1, …
, k=0, 1, …
Функция стоимости.
Как и для одноканальных систем, увеличение коэффициента загрузки ведет к увеличению вероятности отказа системы. С другой стороны, увеличение количества линий обслуживания ведет к увеличению вероятности простоя системы или отдельных каналов. Таким образом, необходимо найти оптимальное количество каналов обслуживания данной СМО. Среднее число свободных линий обслуживания можно найти по формуле ![]() . Введем С(s) – функцию стоимости СМО, зависящую от с1 – стоимости одного отказа (штрафа за невыполненную заявку) и от с2 – стоимости простоя одной линии за единицу времени.
. Введем С(s) – функцию стоимости СМО, зависящую от с1 – стоимости одного отказа (штрафа за невыполненную заявку) и от с2 – стоимости простоя одной линии за единицу времени.
Для поиска оптимального варианта надо найти (и это можно сделать) минимальное значение функции стоимости: С(s) = с1*l*ps+с2*![]() , график которой представлен на рисунке 3.3:
, график которой представлен на рисунке 3.3:
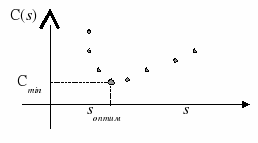
Рисунок 3.3
Поиск минимального значения функции стоимости состоит в том, что мы находим ее значения сначала дляs =1, затем для s =2, потом для s =3, и т.д. до тех пор, пока на каком-то шаге значение функции С(s) не станет больше предыдущего. Это и означает, что функция достигла своего минимума и начала расти. Ответом будет то число каналов обслуживания (значение s), для которого функция стоимости минимальна.
ПРИМЕР.
Сколько линий обслуживания должна содержать СМО с отказами, если l=2треб/час, m =1треб/час, штраф за каждый отказ составляет 7 тыс.руб., стоимость простоя одной линии – 2 тыс.руб. в час?
Решение. y =2/1=2. с1=7, с2=2.
Предположим, что СМО имеет два канала обслуживания, т.е. s =2. Тогда 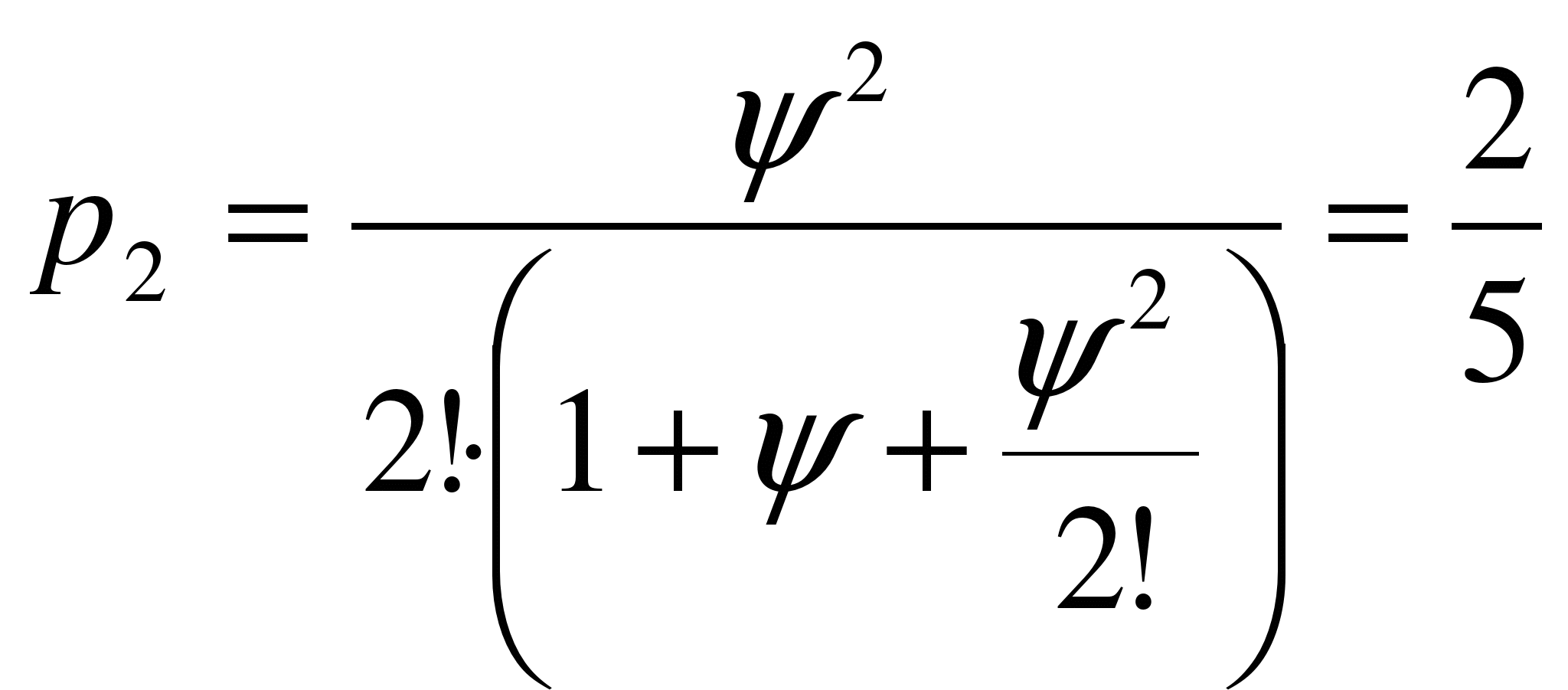 . Следовательно, С(2) = с1*l*p2+с2*(2-y*(1-р2))= =7*2*0.4+2*(2-2*0.6)=7.2.
. Следовательно, С(2) = с1*l*p2+с2*(2-y*(1-р2))= =7*2*0.4+2*(2-2*0.6)=7.2.
Предположим, что s =3. Тогда 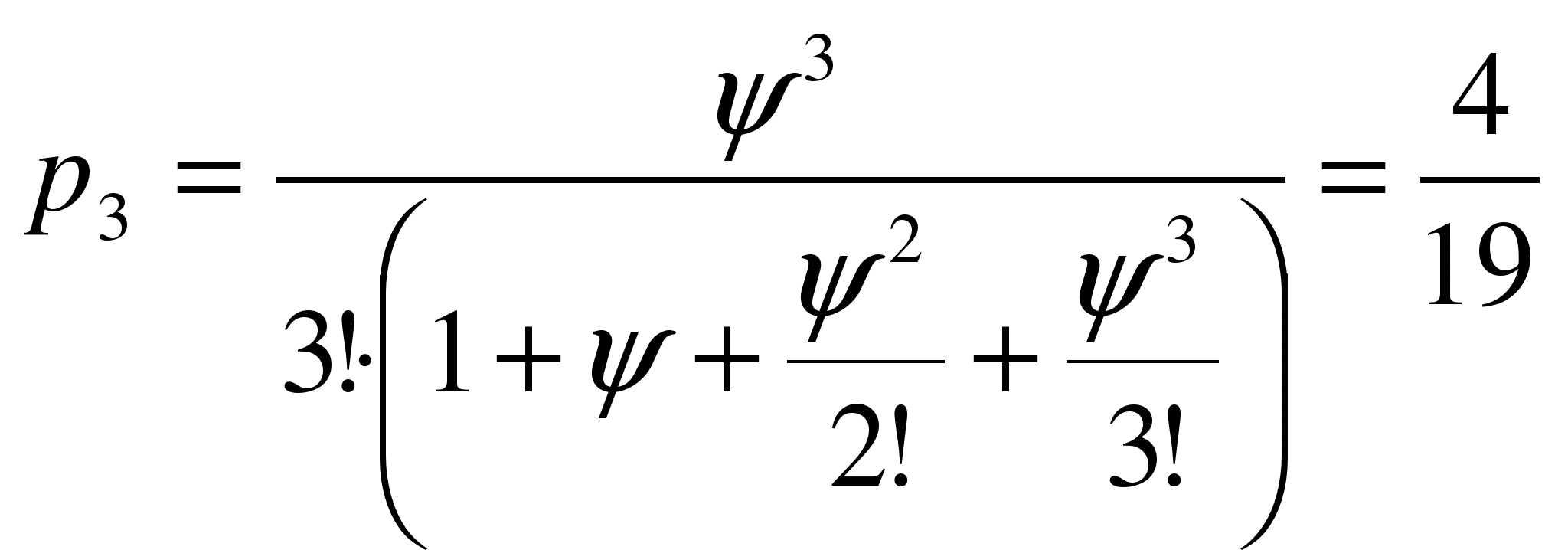 , С(3) = с1*l*p3+с2*
, С(3) = с1*l*p3+с2*![]() =5.79.
=5.79.
Предположим, что имеется четыре канала, т.е. s =4. Тогда 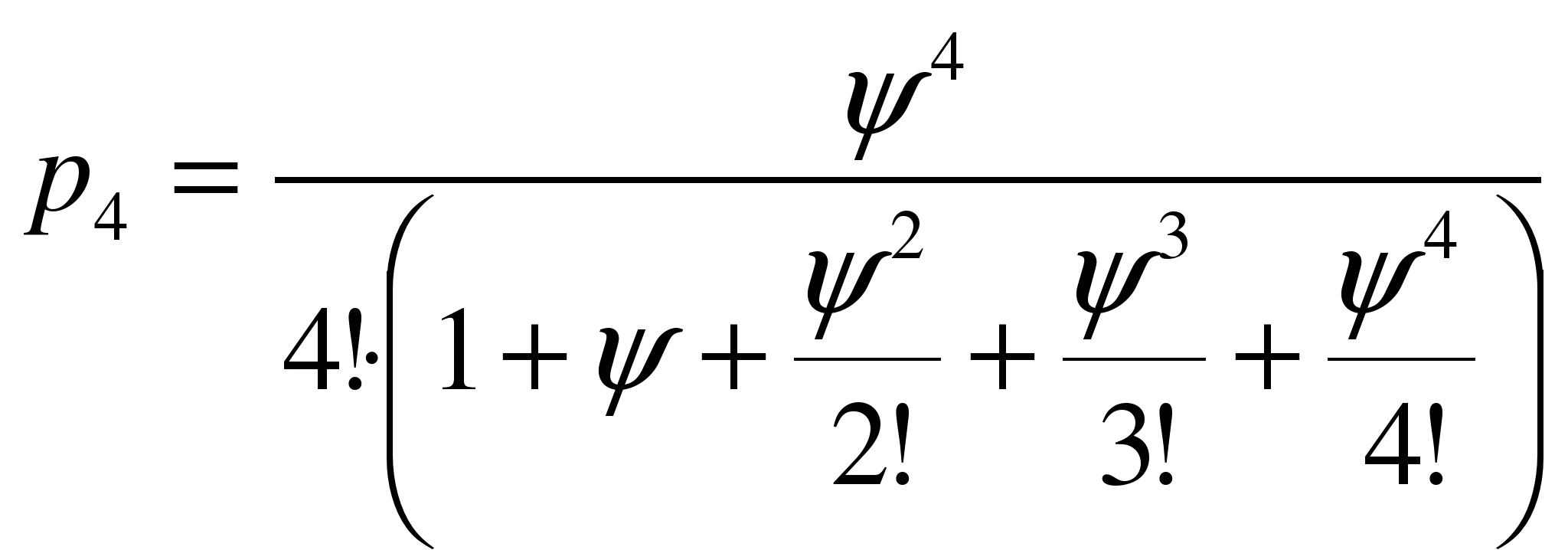 ,
, ![]() , С(4) = с1*l*p4+с2*
, С(4) = с1*l*p4+с2*![]() =5.71.
=5.71.
Предположим, что СМО имеет пять каналов обслуживания, т.е. s =5. Тогда ![]() , С(5) =6.7 – больше предыдущего значения. Следовательно, оптимальное число каналов обслуживания – четыре.
, С(5) =6.7 – больше предыдущего значения. Следовательно, оптимальное число каналов обслуживания – четыре.
3.5.2 Многоканальные СМО с очередью.
Будем рассматривать системы (Р/Е/s):(d/d+s/¥) в предположении, что время обслуживания не зависит от входного потока и все линии работают независимо. Будем говорить, что в системе установилсястационарный режим работы, если среднее число поступающих требований меньше среднего числа требований, обслуженных на всех линиях системы, т.е. l < m * s (или j = y / s < 1). Анализ систем такого рода показывает, что
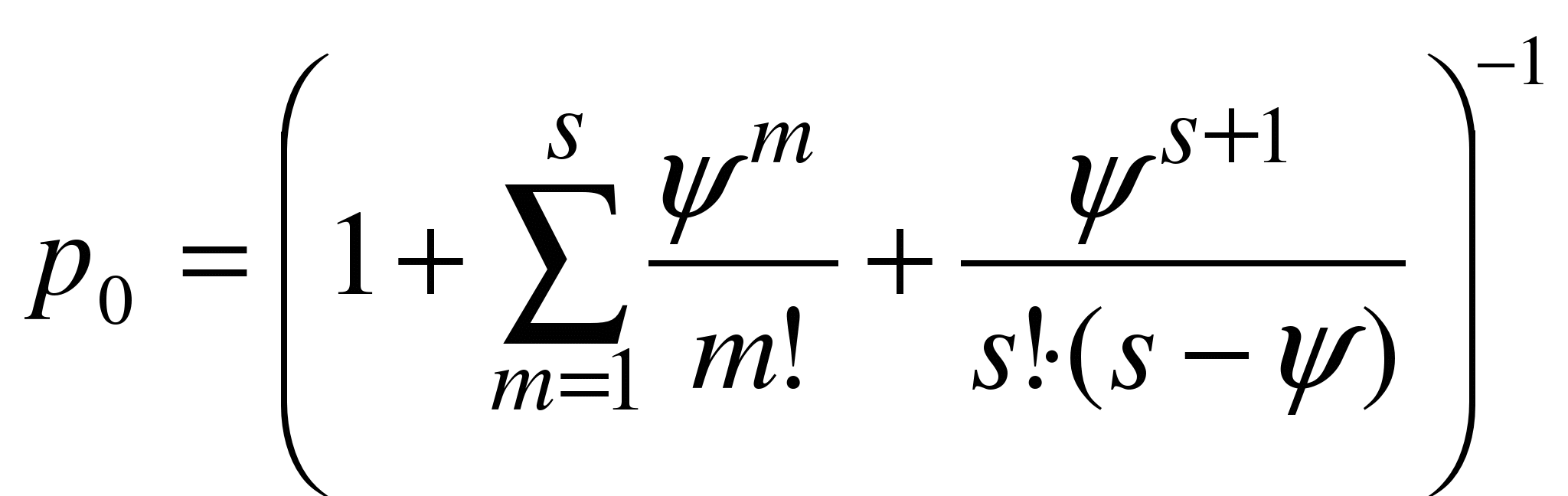 ,
,
а ![]() , для k =1,2,…
, для k =1,2,…
Характеристики.
Как и одноканальные СМО с ожиданием, многоканальные СМО характеризуются некоторыми характеристиками. Нас интересуют средние значения этих величин.
j – количество занятых линий обслуживания, ![]() .
.
r – число свободных линий, ![]() .
.
v – длина очереди, 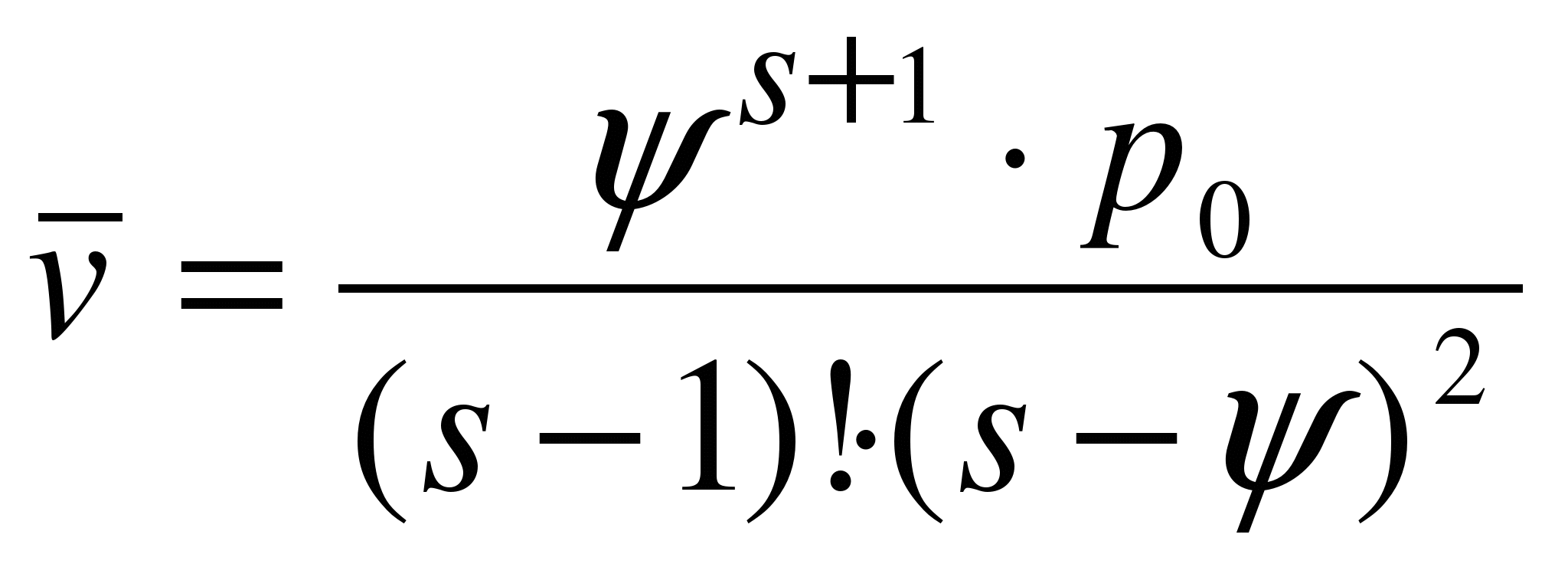 .
.
w – время ожидания начала обслуживания, ![]() .
.
P(w>0) – вероятность ожидания начала обслуживания, 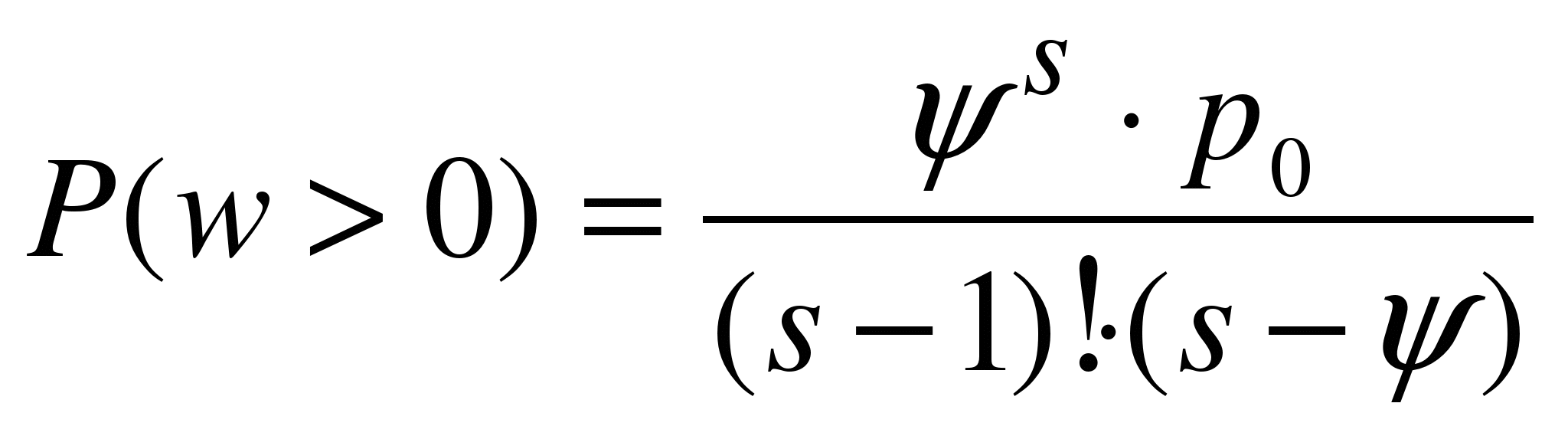 .
.
Последняя характеристика позволяет решать задачу об определении оптимального числа каналов обслуживания с таким расчетом, чтобы вероятность ожидания начала обслуживания была меньше заданного числа. Для этого достаточно просчитать вероятность ожидания последовательно при s =1, s =2, s=3 и т.д.
ПРИМЕР.
СМО – станция скорой помощи небольшого микрорайона. l=3 вызова в час, а m = 4 вызова в час для одной бригады. Сколько бригад необходимо иметь на станции, чтобы вероятность ожидания выезда была меньше 0.01?
Решение. Коэффициент загрузки системы y =0.75. Предположим, что в наличие имеется две бригады. Найдем вероятность ожидания начала обслуживания при s =2. 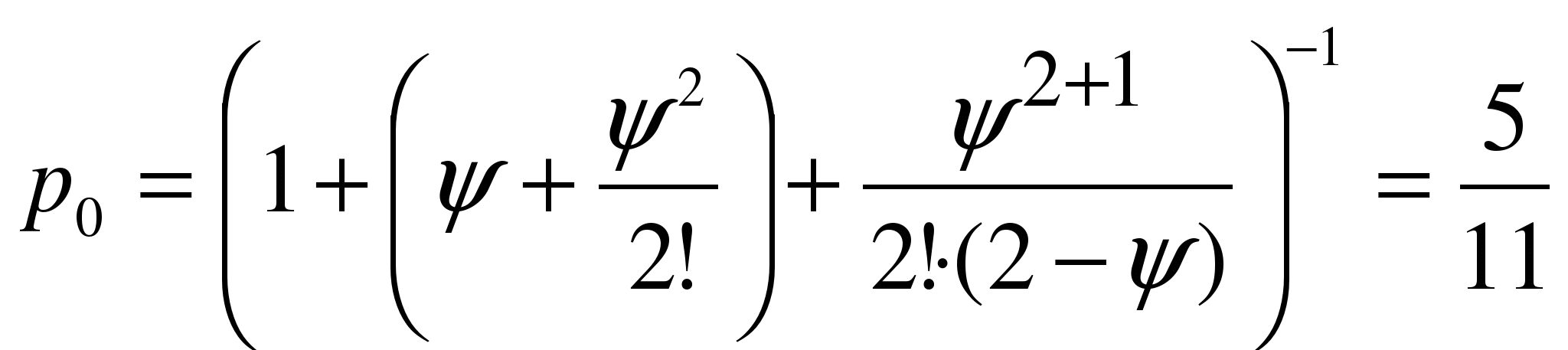 ,
, ![]() .
.
Предположим наличие трех бригад, т.е. s =3. По формулам получим, что р0=8/17, Р(w>0)=0.04>0.01.
Предположим, что на станции четыре бригады, т.е. s =4. Тогда получим, что р0=416/881, Р(w>0)=0.0077<0.01. Следовательно, на станции должно быть четыре бригады.
3.6 Вопросы для самоконтроля
- Предмет и задачи теории массового обслуживания.
- СМО, их модели и обозначения.
- Входной поток требований. Интенсивность входного потока.
- Состояние системы. Матрица и граф переходов.
- Одноканальные СМО с отказами.
- Одноканальные СМО с очередью. Характеристики.
- Стационарный режим работы. Коэффициент загрузки системы.
- Многоканальные СМО с отказами.
- Оптимизация функции стоимости.
- Многоканальные СМО с очередью. Характеристики.
3.7 Упражнения для самостоятельной работы
- Закусочная на АЗС имеет один прилавок. Автомобили прибывают в соответствии с пуассоновским распределением, в среднем 2 автомобиля за 5 минут. Для выполнения заказа в среднем достаточно 1.5 минуты, хотя продолжительность обслуживания распределена по экспоненциальному закону. Найти: а) вероятность простоя прилавка; b) средние характеристики; c) вероятность того, что количество прибывших автомобилей будет не менее 10.
- Рентгеновский аппарат позволяет обследовать в среднем 7 человек в час. Интенсивность посетителей составляет 5 человек в час. Предполагая стационарный режим работы, определить средние характеристики.
- Время обслуживания в СМО подчиняется экспоненциальному закону,
m = 7требований в час. Найти вероятность того, что а) время обслуживания находится в интервале от 3 до 30 минут; b) требование будет обслужено в течение одного часа. Воспользоваться таблицей значений функции ех. - В речном порту один причал, интенсивность входного потока – 5 судов в день. Интенсивность погрузочно-разгрузочных работ – 6 судов в день. Имея в виду стационарный режим работы, определить все средние характеристики системы.
- Какое оптимальное число каналов обслуживания должна иметь СМО, если l=3, m =2, штраф за каждый отказ равен 5, а стоимость простоя одной линии равна 2?
- Какое оптимальное число каналов обслуживания должна иметь СМО, если l=3, m =1, штраф за каждый отказ равен 7, а стоимость простоя одной линии равна 3?
- Какое оптимальное число каналов обслуживания должна иметь СМО, если l=4, m =2, штраф за каждый отказ равен 5, а стоимость простоя одной линии равна 1?
- Определить число взлетно-посадочных полос для самолетов с учетом требования, что вероятность ожидания должна быть меньше, чем 0.05. При этом интенсивность входного потока 27 самолетов в сутки, а интенсивность их обслуживания – 30 самолетов в сутки.
- Сколько равноценных независимых конвейерных линий должен иметь цех, чтобы обеспечить ритм работы, при котором вероятность ожидания обработки изделий должна быть меньше 0.03 (каждое изделие выпускается одной линией). Известно, что интенсивность поступления заказов 30 изделий в час, а интенсивность обработки изделия одной линией – 36 изделий в час.
- Непрерывная случайная величина Х распределена по показательному закону с параметром l=5. Найти функцию распределения, характеристики и вероятность попадания с.в. Х в интервал от 0.17 до 0.28.
- Среднее число вызовов, поступающих на АТС за одну минуту, равно 3. Считая поток пуассоновским, найти вероятность того, что за 2 минуты поступит: а) два вызова; б) меньше двух вызовов; в) не менее двух вызовов.
- В ящике 17 деталей, из которых 4 – бракованные. Сборщик наугад извлекает 5 деталей. Найти вероятность того, что а) все извлеченные детали – качественные; б) среди извлеченных деталей 3 бракованных.
- Сколько каналов должна иметь СМО с отказами, если l=2треб/час, m=1треб/час, штраф за каждый отказ составляет 8т.руб., стоимость простоя одной линии – 2т.руб. в час?
